矩阵分析复习

一、题目类型与分值

  1. 计算解 (4小题) ，共45分;
  2. 问题求解题 (2小题) ，共25分;
  3. 证明题 (3小题) ，共30分

二、复习提纲

  1. 矩阵的Hadamard积和Kronecker 积

Jordan标准型

image-20231118193059913

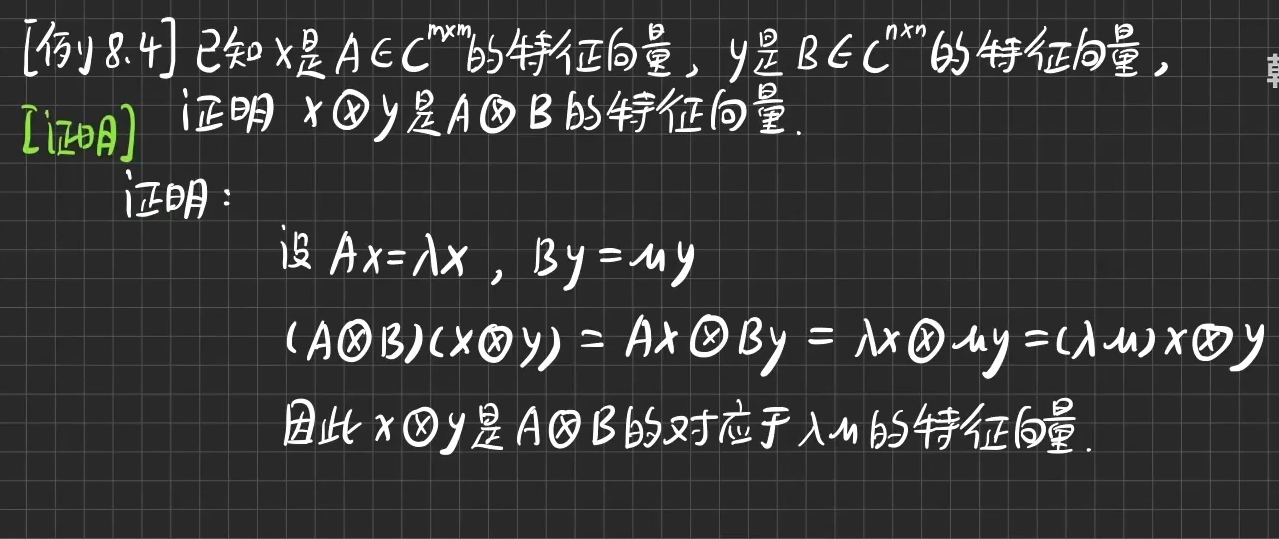
image-20231118193133935

  1. 矩阵的迹

  2. 求实矩阵函数的 Jacobian 矩阵和梯度矩阵:

  3. 求矩阵 $A$ 的Moor-Penrose逆 $ A^{\dagger } $

满秩分解法

  1. 求到矩阵 $A$ 列空间上的投影算子和正交投影算子

投影算子： $$ P=AA^{\dagger } $$ 正交投影算子： $$ I-P=I-AA^{\dagger } $$

  1. 求与A最接近的正交矩阵

考虑正交强迫一致问题： $$ \min_{Q^TQ=I} \left | A-BQ \right | ^{2} {F} $$ 化简： $$ \left | A-BQ \right | ^{2} {F}=tr(AA^T)-2tr(Q^TB^TA)+tr(Q^TB^TBQ) $$ 即求： $$ \min{Q^TQ=I} tr(Q^TB^TA) $$ 设 $ B^TA = U\Sigma V^T$ ，正交矩阵$ Z=V^TQ^TU $ ，则有： $$ tr(Q^TB^TA) = tr(Q^TU\Sigma V^T) = tr(V^TQ^TU\Sigma) = tr(Z\Sigma) $$ 其中： $$ tr(Z\Sigma)=\sum{i=1}^{n}z_{ii}\sigma_{i} \le \sum_{i=1}^{n}\sigma_{i} $$ 当且仅当 $ z_{ii} = 1 $ 时等号成立，即 $ Z=I, Q=UV^T$

特例：当 $ B=I $ 时，$ Q=UV^T $ 即 $ A $ 最接近的正交矩阵。

  1. 正则化非负矩阵分解的迭代法则 (加法和乘法迭代法则) :

平方 Euclidean 距离 $$ \min_{A,S} D_{E}(X||AS) = \frac{1}{2} \left | X-AS \right | ^2_{F} $$ 迭代公式（加法形式）： $$ \left{\begin{matrix} a_{ik} \longleftarrow a_{ik} - \mu_{ik} \frac{\partial D_E(X || AS)}{\partial a_{ik}} \s_{kj} \longleftarrow s_{kj} - \eta_{kj} \frac{\partial D_E(X || AS)}{\partial s_{kj}}

\end{matrix}\right. $$

其中： $$ \left{\begin{matrix} \frac{\partial D_E(X || AS)}{\partial A} = -(X-AS)S^T \\frac{\partial D_E(X || AS)}{\partial S} = -A^T(X-AS)

\end{matrix}\right. $$ 则可以化简为乘法形式，令： $$ \left{\begin{matrix} \mu_{ik}=\frac{a_{ik}}{[ASS^T]{ik}} \\eta{kj}=\frac{s_{kj}}{[A^TAS]_{kj}}

\end{matrix}\right. $$

乘法形式： $$ \left{\begin{matrix} a_{ik} \longleftarrow a_{ik} \frac{[XS^T]{ik}}{[ASS^T]{ik}} \ s_{kj} \longleftarrow s_{kj} \frac{[A^TX]{kj}}{[A^TAS]{kj}} \end{matrix}\right. $$ K-L 散度

  1. $ L_1 $ 正则化最小二乘问题解的充要条件;

$ L_1 $ 正则化最小二乘问题： $$ minJ(\lambda, x) = \frac{1}{2} \left | y-Ax \right | _{2} ^{2} + \lambda \left | x \right | _{1} $$ 次梯度向量： $$ \nabla_x J(\lambda, x) = -A^{T}(y-Ax) + \lambda \nabla_x \left | x \right | _{1} $$

设 $ c = A^{T}(y-Ax) $，则 $L_1$ 正则化最小二乘问题的平稳条件（充要条件）： $$ c = \lambda \nabla_x \left | x \right | _{1} $$

其中： $$ \nabla_{x_{i}} \left | x \right | {1} = \left{\begin{matrix} {+1} \qquad \quad x{i} > 0 \\left [ -1, +1 \right ] \qquad x_{i} = 0 \{-1} \qquad \quad x_{i} < 0 \end{matrix}\right. $$ 即： $$ c_i= \left{\begin{matrix} {+\lambda} \qquad \quad x_{i} > 0 \\left [ -\lambda, +\lambda \right ] \qquad x_{i} = 0 \{-\lambda} \qquad \quad x_{i} < 0 \end{matrix}\right. $$

  1. Rayleigh商和广义Rayleigh商的最小化或最大化问题的解:

Hermitian 矩阵 $ A $ 的 Rayleigh 商为： $$ R(A,x)=\frac{x^HAx}{x^Hx} $$ 将最小二乘问题简化，令 $ x^Hx=1 $ ，此时 $ R(A,x)=x^HAx $

构造Lagrange乘子函数 $ L(x,\lambda) = x^HAx - \lambda (x^Hx-1) $

对 $ x $ 求梯度并令其为 $0$ ，得到 $ 2Ax - 2\lambda x =0 $

等价于 $ \lambda_{i} $ 为矩阵 $A $ 第 $ i $ 个特征值，$ x_i $ 为其特征向量，故： $$ R(A,x_i)=\lambda_i $$ 得到结论：当取 $A $ 的最大特征向量 $ x_{max} $ 时，Rayleigh 商有最大值即为 $ \lambda_{max} $ ；同理取 $A $ 的最小特征向量 $x_{min}$ 时，Rayleigh 商有最小值即为 $ \lambda_{min} $

广义 Rayleigh 商中，如果 $B$ 为正定矩阵： $$ R(A,B,x)=\frac{x^HAx}{x^HBx} $$ 设新的向量 $ \tilde{x}=B^{1/2}x $ ，代入得： $$ R(A,\tilde{x})=\frac{\tilde{x}^H(B^{-1/2})^HAB^{-1/2}\tilde{x}}{\tilde{x}^H\tilde{x}} $$ 故矩阵对 $(A,B)$ 的广义 Rayleigh 商即为 $ (B^{-1/2})^HAB^{-1/2}$ 的标准 Rayleigh 商

若 $ (B^{-1/2})^HAB^{-1/2} $ 的特征值分解为： $$ (B^{-1/2})^HAB^{-1/2}\tilde{x}=\lambda \tilde{x} \ B^{-1}Ax=\lambda x \ Ax=\lambda Bx $$ 此表明矩阵 $ (B^{-1/2})^HAB^{-1/2}$ 的特征值分解与矩阵对 $(A,B)$ 的广义特征分解等价。故 $ x$ 取矩阵对 $(A,B)$ 的广义特征值对应的最大特征向量时，广义 Rayleigh 商最大化。

  1. 实对称矩阵或Hermitian矩阵的特征值必为实数

证明 Hermitian 矩阵特征值均为实数，属于不同特征值的特征向量正交

一、原式子： $$ Ax=\lambda x $$ 两边取共轭转置： $$ x^HA^H=\bar{\lambda} x^H $$ 两边右乘 $x$ ： $$ x^HA^Hx=\bar{\lambda}x^Hx \ x^HAx=\bar{\lambda}x^Hx \ \lambda x^Hx=\bar{\lambda} x^Hx $$ $x$ 非0向量，则 $ \lambda - \bar{\lambda} = 0$ ，故 Hermitian 矩阵的特征值必为实数

二、证明正定矩阵的特征值都大于0

原式子： $$ Ax=\lambda x \ x^TAx=\lambda x^Tx $$ 由于 $ x^TAx > 0 $，又有 $x$ 非0向量，$ x^Tx >0 $

故： $$ \lambda =\frac{x^TAx}{x^Tx} > 0 $$ 得证

  1. 总体最小二乘问题的解。

如何解